#rst2hooktail_source
============================================================ ビオ・サバールの法則とその応用 ============================================================
円電流の作る磁場をビオ・サバールの法則を用いて直接積分して求めます。
導入 ======================== 電流は流れるとき、必ず磁場を伴って流れています。 それを表す法則は、ふたつありまして、 一方は「アンペールの法則」、もう一方は、「ビオ・サバールの法則」と呼ばれています。 ここでは、ビオ・サバールの法則を使って、簡単な例に適用してみます。
ビオ・サバールの法則 ========================
原点に微小な電流要素 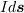 を考えます。ただし
を考えます。ただし 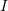 は電流の大きさで、微小方向ベクトルは電流の向きを表す方向
ベクトル
は電流の大きさで、微小方向ベクトルは電流の向きを表す方向
ベクトル 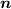 を用いて、
を用いて、 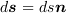 と表される。この微小電流要素が、位置
と表される。この微小電流要素が、位置  に作る磁場
に作る磁場 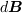 は、
は、
tex>
d \bm{B} = \frac{\mu_0I}{4 \pi}\ \frac{d \bm{s} \times \bm{r}}{ | \bm{r} |^3 } = \frac{\mu_0I}{4 \pi}\ \frac{d \bm{s} \times \hat{ \bm{r} } }{ | \bm{r} |^2 } \tag{#def(biot)}/tex>
となります。ただし 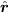 は位置ベクトル方向を向いた単位ベクトルとしました。
は位置ベクトル方向を向いた単位ベクトルとしました。
円電流が作る磁場 ========================
いまxy平面内に半径  の円電流を考えます。この円電流が作る磁場をビオ・サバールの法則で計算してみます。
の円電流を考えます。この円電流が作る磁場をビオ・サバールの法則で計算してみます。
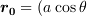 にある微小電流が (この時、微小接線ベクトル
にある微小電流が (この時、微小接線ベクトル 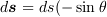 です)
です) 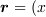 の位置
に(最後は円筒座標を使いました)作る磁場は、式 (#ref(biot)) より、
の位置
に(最後は円筒座標を使いました)作る磁場は、式 (#ref(biot)) より、
tex>
d \bm{B} = \frac{\mu_0I}{4 \pi} \ \frac{d \bm{s} \times (\bm{r}-\bm{r_0})}{ | \bm{r}-\bm{r_0} |^3 }/tex>
今、
tex> d \bm{s} \times (\bm{r}-\bm{r_0})= \begin{vmatrix}
\bm{i}&\bm{j}&\bm{k} \\
- ds \sin \theta & ds \cos \theta & 0 \\ x - a \cos \theta & y - a \sin \theta & z \end{vmatrix} = \begin{pmatrix} z \cos \theta \\ z \sin \theta \\ a-y \sin \theta -x \cos \theta \end{pmatrix} ds = \begin{pmatrix} z \cos \theta \\ z \sin \theta \\ a-r \cos (\theta-\phi) \end{pmatrix} ds
/tex> で、
tex> |\bm{r}-\bm{r_0}|^2 = |\bm{r}|^2+|\bm{r_0}|^2-2\bm{r} \cdot \bm{r_0}=r^2 +z^2 +a^2 -2ra \cos (\theta -\phi)
/tex>
です。これを用いて、まずz方向の磁場 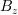 を求めます。微小距離
を求めます。微小距離 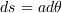 と置けるのでθの積分にすることができて、
と置けるのでθの積分にすることができて、
tex> B_z =\int d B_z = \frac{\mu_0I}{4 \pi} \int^{2\pi}_0 \frac{a-r \cos (\theta -\phi)}{(r^2 +z^2 +a^2 -2ra \cos (\theta -\phi)\ )^{\frac{3}{2}}}a d \theta
/tex>
同様にx方向、y方向も書くと、
tex> B_x =\int d B_x = \frac{\mu_0I}{4 \pi} \int^{2\pi}_0 \frac{z \cos \theta}{(r^2 +z^2 +a^2 -2ra \cos (\theta -\phi)\ )^{\frac{3}{2}}}a d \theta
/tex>
tex> B_y =\int d B_y = \frac{\mu_0I}{4 \pi} \int^{2\pi}_0 \frac{z \sin \theta}{(r^2 +z^2 +a^2 -2ra \cos (\theta -\phi)\ )^{\frac{3}{2}}}a d \theta
/tex>
です。おそらくこの積分は解けません。
円電流が作る磁場(原点では) ========================
解けないとは言いましたが、二つの特別な場合を計算してみます。
まず 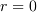 の時は簡単です。まずz方向について見てみます。
の時は簡単です。まずz方向について見てみます。
tex> B_z = \frac{\mu_0I}{4 \pi} \int^{2\pi}_0 \ \frac{a-r \cos (\theta -\phi)}{(r^2 +z^2 +a^2 -2ra \cos (\theta -\phi)\ )^{\frac{3}{2}}}a d \theta = \frac{\mu_0I}{4\pi} \int ^{2\pi}_0 \ \frac{a^2}{(a^2+z^2)^{\frac{3}{2}}} d \theta =\frac{\mu_0I}{2} \ \frac{a^2}{(a^2+z^2)^\frac{3}{2}}
/tex>
となり、またx方向、y方向は対称性から0になります。
さらに特別な場合、コイルの円の中心 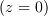 では
では 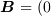 となります。
となります。
円電流が作る磁場(十分に遠方では) ========================
十分に遠方 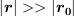 では、分母を近似することができます。
では、分母を近似することができます。
tex> \frac{1}{|\bm{r}-\bm{r_0}|^2} =\frac{1}{(r^2 +z^2 +a^2 -2ra \cos (\theta -\phi)\ )^{\frac{3}{2}}} =(r^2+z^2)^{-\frac{3}{2}} \ (1-\frac{2ar}{r^2+z^2} \cos (\theta - \phi)+\frac{a^2}{r^2+z^2})^{-\frac{3}{2}}
/tex>
ここで 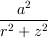 は二次の微小量なので無視し、テイラー展開
は二次の微小量なので無視し、テイラー展開 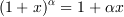 を用いると、
を用いると、
tex> \frac{1}{|\bm{r}-\bm{r_0}|^2} =(r^2+z^2)^{-\frac{3}{2}}(1-\frac{2ar}{r^2+z^2} \cos (\theta - \phi))^{-\frac{3}{2}} =(r^2+z^2)^{-\frac{3}{2}}(1+\frac{3}{2} \ \frac{2ar}{r^2+z^2} \cos (\theta - \phi))
/tex>
となります。これを用いてz方向成分を求めると、
tex> B_z &= \frac{\mu_0I}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 (a-r \cos (\theta -\phi))(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi))a d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 r(- \cos (\theta -\phi)+\frac{a}{r})(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi)) d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 r(-1+\frac{3a^2}{r^2+z^2})\cos (\theta -\phi) +a -\frac{3ar^2}{r^2+z^2}\cos^2 (\theta -\phi) d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} [ ar(\frac{1}{r} -\frac{3r}{2(r^2+z^2)}) (\theta-\phi) ]^{2\pi}_0 \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \{ 2\pi ar (\frac{r^2+z^2}{r(r^2+z^2)}-\frac{\frac{3}{2}r^2}{r(r^2+z^2)})\} \\ &= \frac{\mu_0Ia}{2(r^2+z^2)^{\frac{3}{2}}} ( ar \frac{z^2-\frac{1}{2}r^2}{r(r^2+z^2)}) \\ &= \frac{\mu_0Ia^2}{2(r^2+z^2)^{\frac{5}{2}}} (z^2-\frac{1}{2}r^2)
/tex>
ふう疲れた、とにかくこうなるわけですよ。
まだ、x方向とy方向が残っています。でも安心してください。x方向は 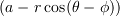 を
を 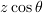 で置き換えるだけです。
で置き換えるだけです。
tex> B_x &= \frac{\mu_0I}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \cos \theta(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi))a d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \cos \theta(1+\frac{3a}{r^2+z^2} r\cos (\theta - \phi)) d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \cos \theta(1+\frac{3a}{r^2+z^2} (x \cos \theta + y \sin \theta) d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z (\cos \theta +\frac{3ax}{r^2+z^2} \cos^2 \theta + \frac{3ax}{r^2+z^2} \sin \theta \cos \theta) d \theta \\ &= \frac{\mu_0Ia}{4 \pi(r^2+z^2)^{\frac{3}{2}}} [ z \frac{3ax}{2(r^2+z^2)} \theta ]^{2\pi}_0 \\ &= \frac{3\mu_0Ia^2xz}{4 (r^2+z^2)^{\frac{5}{2}}}
/tex>
y方向についてはこれのxをyで、yはxで 置き換えればいいので、
tex> B_y &= \frac{\mu_0I}{4 \pi(r^2+z^2)^{\frac{3}{2}}} \int^{2\pi}_0 z \sin \theta(1+\frac{3ar}{r^2+z^2} \cos (\theta - \phi))a d \theta \\ &= \frac{3\mu_0Ia^2yz}{4 (r^2+z^2)^{\frac{5}{2}}}
/tex>
まとめると、
tex> \bm{B}=\frac{\mu_0Ia^2}{(r^2+z^2)^{\frac{5}{2}}}\begin{pmatrix} \frac{3}{4}xz \\ \frac{3}{4}yz \\ \frac{3}{4}z^2-\frac{1}{4}(x^2+y^2+z^2) \end{pmatrix}
/tex>
であり、成分としてまとめると、
tex> B_n=\frac{3\mu_0Ia^2}{4(r^2+z^2)^{\frac{5}{2}}} (x_n x_3 - \frac{1}{3}(x_1^2+x_2^2+x_3^2)\delta_{3n}) \ \ \ \ \ (n=1,2,3)
/tex>
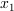 は、それぞれ
は、それぞれ  をあらわし、
をあらわし、 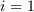 にたいし
にたいし
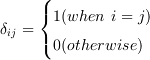 となり、これはクロネッカーのデルタという名前です。
となり、これはクロネッカーのデルタという名前です。
@@author:クロメル@@ @@accept:2007-02-16@@ @@category:電磁気学@@ @@id:bioSavar@@