最近傍決定則では未知パターンに最もユークリッド距離の 近いサンプルが属するクラスタに未知パターンを分類しました. しかし,例えば,
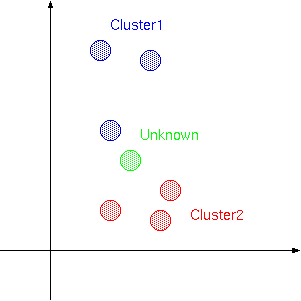
のような場合,最も近いサンプルが属するクラスタはCluster1ですが, それでは未知パターンはCluster1に属するかというと,直感的にはCluster2に属する気がします.
サンプルがそのクラスタを代表する理想的なものであればいいのですが, そういう訳には行きません.例えば,数字を書いても「1」のような「7」を書く人もいるでしょう. そのような「7」がサンプルとして混ざっていると,未知パターンが入力されたときに, 最も近いサンプルが「7」に属していても手放しにそれが「7」だと決めつけるのは危険です.
これは少々極端な例ではありますが,最も近いサンプル1つに判断が委ねられる以上, そのような可能性をはらんでいる事は否めません.
そこで,k-最近傍決定則は最も近いサンプルの属するクラスタではなく, 「最も近いk個のサンプルの中で最も多いサンプルが属するクラスタ」に 未知パターンも属するという風に考えます.こう考えると上の図で未知パターンは めでたくCluster2に属してくれます.
最近傍決定則はそもそも「似ているものは近くに配置されるハズだ」という 観点から始まっていますので,見方を変えると,「ClusterAに属するサンプル の周りで一番多いのはClusterAのサンプルである」ということになります. また,k-最近傍決定則において,kが1のときは最近傍決定則と同じになりますので, 最近傍決定則はk-最近傍決定則の特別な場合と考える事もできます.
for(i=0; i<k; i++){
dist[i] = -1.0;
indexcluster[i] = -1;
}
最も近いk個のサンプルとの距離とそれに対応するクラスタのインデックスを保持する distとindexclusterという配列を初期化しています.(全ての距離を求めてからソートする方が早い気もします)
for(i=0; i<num; i++){
for(j=0; j<cluster[i]->num; j++){
double maxdist=.0;
double d;
int maxindex;
for(m=0; m<k; m++){
if(dist[m] < .0){
maxindex = m;
break;
}
if(maxdist <= dist[m]){
maxdist = dist[m];
maxindex = m;
}
}
d = 0.0;
for(m=0; m<cluster[i]->v[j]->size; m++){
d += SQR(x->v[m] - cluster[i]->v[j]->v[m]);
}
if((d>SQR(maxd)) || ((maxdist<d) && (dist[maxindex]>=0))) continue;
indexcluster[maxindex] = i;
dist[maxindex] = d;
}
}
上から3つめのfor文の中で最も距離の遠いものを探します. もしまだk個のデータが入っていなければ(初期化されたままのものがあれば) その要素を使います.許容できる距離以上離れていれば何もせずに次に進み, そうでなければ現在のk個の内の最も距離が離れているサンプルと比較し, 現在注目しているサンプルの方が近ければ更新します.また,まだk個のデータがdistやindexcluster に入っていなければそのまま更新します.
for(i=0; i<num; i++) count[i] = 0;
for(i=0; i<k; i++){
if(indexcluster[i] < 0) continue;
count[indexcluster[i]]++;
}
もっとも近いk個が得られましたので,最も多くのサンプルが属するクラスタを求めます. そこでクラスタの数だけ要素を持つ配列countを初期化し,数えていきます.
maxcount = checkmulti = 0;
for(i=0; i<num; i++){
if(maxcount < count[i]){
maxcount = count[i];
index = i;
checkmulti = 0;
}else if(maxcount == count[i]){
checkmulti = 1;
}
}
if(checkmulti) index = -1;
ここで最も多くのサンプルが属するクラスタを求めているのですが, 2つ以上のクラスタが同時に勝者となってしまった場合識別不能としています.