Simpson則(シンプソン則)を用いて定積分を求めてみます.
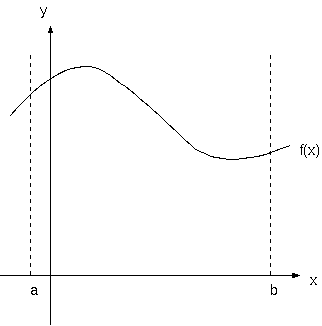
このようなf(x)を積分区間[a,b]で積分するとします. このとき十分大きな数nを考え,積分区間をn等分します. PCでは無限を考えることができないために有限個にしか分割できませんが, nを大きくすることで誤差を小さくすることができます.
ここでn等分された区間のうちの1つを拡大して見てみます.
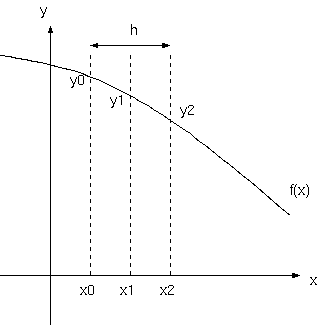
分割された内の1つの区間[x0,x2]を考え,区間の幅をhとします. [x0,x2]の中間値をx1とし,f(x0),f(x1),f(x2)をそれぞれ y0,y1,y2とします.
よく積分の説明で,矩形を考えて幅をゼロに近付けるというのがありますが, それができるのは無限という概念が存在するからで,有限の値しか 扱えないPCで矩形を考えては大きなすき間が空いてしまい, 誤差が大きくなる,または分割数をかなり大きくしなければならなくなります. そのためこの(x0,y0),(x1,y1),(x2,y2)の三点を通る2次曲線で近似します. そうすることですき間を極めて小さくできると考えられます.
とおいてx1を中心とした二次式を考えます.こうすると計算が楽になります.
ここで,
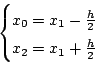
より,
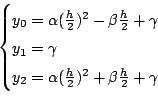
となり,
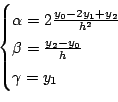
これより[x0,x2]の範囲で積分すると,
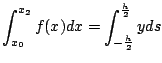
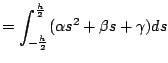
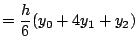
ここで積分区間をn分割したときのi番目の区間を積分した値は,
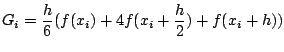
となり,積分区間[a,b]で積分すると,
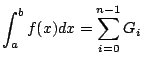
以上長くなりましたが,実装するのは簡単です.
double Simpson(double (*f)(double x), double x0, double x1, int num)
{
double h;
double sum = 0.0, x;
int i;
h = (x1 - x0);
if(num) h /= num;
x = x0;
for(i=0; i<num; i++){
sum += (*f)(x) + 4.*(*f)(x + h/2) + (*f)(x + h);
x += h;
}
return sum*h/6;
}
使いまわしがきくように関数ポインタを使用しました. 関数ポインタとは関数をアドレスで渡して使う方法で,動的に使用する関数を変更することが出来る という便利な方法です.main関数より,
double f1(double x)
{
return x;
}
double f2(double x)
{
return 4 / (1 + x * x);
}
という2つの関数を順に積分しています.関数名だけを書けば,それが関数のアドレスとなりますので,
Simpson(f1, 2, 5, 1000);
のようにすると,
for(i=0; i<num; i++){
sum += (*f)(x) + 4.*(*f)(x + h/2) + (*f)(x + h);
x += h;
}
の部分は
for(i=0; i<num; i++){
sum += f1(x) + 4.*f1(x + h/2) + f1(x + h);
x += h;
}
と同じ処理をします.