Heun法によって 随分と精度の高い常微分方程式の数値解を得ることができるようになりましたが, もっと精度の良い4次のRunge-Kutta法を作成してみます. Runge-Kutta法は5次以上のものもあるようなのですが,4次のものが優れており, 4次のRunge-Kutta法に手を加える形になるようです. ところで自分は4次のRunge-Kutta法を導出することはできませんので, 以下の図等で直感的に精度が良さそうだと思って頂ければ幸いです.
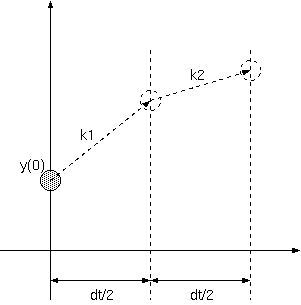
まずEuler法のときのような感じで 幅を半分で計算し傾きk1を算出します.幅dt/2の間,yの関数の傾きはk1で あったと仮定しy(dt/2)の値を仮定します.その後y(dt/2)を初期値とし, dt/2からdtまでの間のyの関数の傾きk2を算出します.Euler法であれば これを解とし,どんどん先に進んでいくわけですが,Runge-Kutta法はまだ続きます.
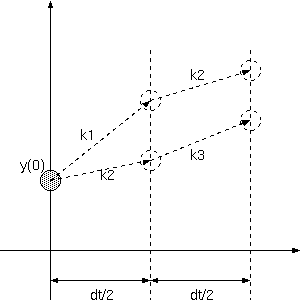
0からdt/2までの範囲でyの関数の傾きが先程求まった傾きk2であると仮定し もう一度y(dt/2)を求めてみます.その上で新たに求まったy(dt/2)を使い, 傾きk3を求めて再びy(dt)を算出します.
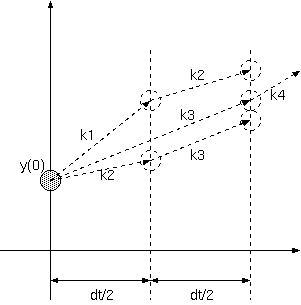
今度は先程求まった傾きk3が0からdtの範囲の傾きであると仮定し, y(dt)を求めます.そしてその値より傾きk4を算出します.以上の4つの傾き k1,k2,k3,k4を用いて,
のようにし,0からdtまでの傾きを算出し,最終的なy(dt)を決定します. 式で書くと次のようになります.
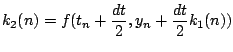
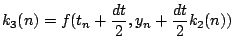
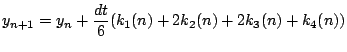
ここでk2とk3は共にdt/2の部分での傾きです. そう考えると数値積分であるSimpson則の式,
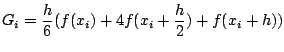
と非常に似ている事が判ります. ところで微分方程式を解くということは実は積分しているという事です. 傾きを出して幅を掛け,高さを求めるというのも正に積分です. とすると,数値積分のSimpson則の式と似ている事もうなずけ, いきなりk2やk3を2倍したりしている事にもある程度納得できます. しっかりと導出しようとすると大変な4次のRunge-Kutta法ですが, Simpson則と絡める事で,Runge-Kutta法を使うには困らない程度の 理解はできたと思います.ちなみにEuler法は積分の矩形公式,Heun法は積分の台形公式に それぞれ対応します.
それではソースコードを見てみます.
h = (tn - t0);
if(div) h /= div;
t = t0;
for(i=0; i<div; i++){
for(j=0; j<num; j++){
k1[j] = (*f[j])(t, x);
temp[j] = x[j] + h*k1[j]/2;
}
for(j=0; j<num; j++){
k2[j] = (*f[j])(t+h/2, temp);
}
for(j=0; j<num; j++){
temp[j] = x[j] + h*k2[j]/2;
}
for(j=0; j<num; j++){
k3[j] = (*f[j])(t+h/2, temp);
}
for(j=0; j<num; j++){
temp[j] = x[j] + h*k3[j];
}
for(j=0; j<num; j++){
k4[j] = (*f[j])(t+h, temp);
x[j] += (k1[j] + 2*k2[j] + 2*k3[j] + k4[j])*h/6;
}
t += h;
}
関数の引数は全く同じです.ただ,k1,k2,k3,k4と 確保しておく傾きの数が増えましたのでメモリの確保やループが増えています. 連立の数を自由に指定することができるように,関数ポインタを使ったり, 初期値を配列で渡したりしているためにごちゃごちゃしてしまいましたが, 基本的に公式をそのまま計算しています.