最近傍決定則やk-最近傍決定則 によりパターンを識別する事ができるようになりました. これらの方法は大変シンプルな考え方でありながら,サンプルが充実していれば かなりの精度で識別が可能だと考えられます.しかし問題点として, サンプル全てを保持しておかなければならない事,次元数が増え,サンプル数が増えると 計算量が膨大になる事が挙げられます.
ここで最近傍決定則のように,パターンに最も距離の近いクラスタを選ぶという作業は 見方を変えると,異なるクラスタのサンプル間において, 垂直二等分線を考え,領域を分けるという事になります.
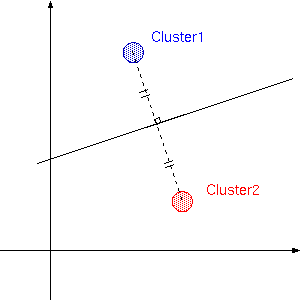
ということは,この境界線を知ることができれば, サンプルのデータは不要と考えることができ,Perceptronはこの境界線を 学習によって得ることができます.ただし,Perceptronは上の図のような垂直二等分線を得る訳ではなく, 学習であたえられたデータ全てが分割できるような線を適当に探します.つまり,
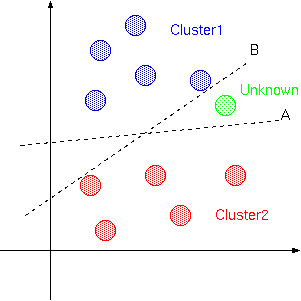
理想的にはCluster1とCluster2は境界Aで分割されて欲しくても, 図のようなサンプルで学習を行った場合境界Bで分割されることもあるということです. そのため図のように未知データが入って来たとき,理想的にはCluster1と判断されるハズが, Cluster2と判断されるかもしれないということです.したがって,学習は偏りなく, 十分に行う必要があります.
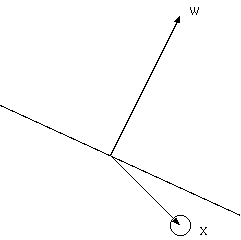
さて,上の図における境界線を学習するために生理学におけるニューロンやシナプスを模した ネットワークモデルを考えます.
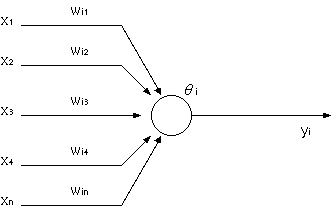
丸をニューロン,線をシナプスだと考えます. 他のニューロンより信号xが伝わり,wの重み付けがされてニューロンに伝わります. 実際には電位として信号が伝わっているようですが,この電位がニューロンにおいて, ある閾値を越えるとそのニューロンは活性化(発火)します.
このモデルより,人工的に次のようなネットワークを作成します.
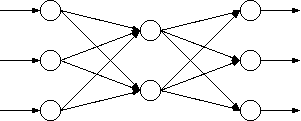
左より「入力層」,「中間層」,「出力層」といいます. この出力層のユニット(ニューロン)が1つの場合,これを単純パーセプトロンと呼びます. 入力層と中間層,中間層と出力層の間の矢印一つ一つにそれぞれ異なる 重みが存在します.パーセプトロンは学習によってこの重みを学習します. しかし,学習するのは中間層と出力層の間の重みだけで, 入力層と中間層の間の重みは固定であるため,実質3層ではなく,2層であると 考えられます.
実質2層ということで「入力層」と「出力層」,その間を繋ぐ可変荷重を考えます. 入力層のユニット数は扱いたいパターンの次元に相当します.
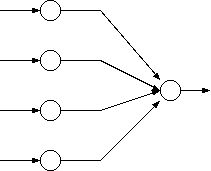
入力層において入力信号は素通りしますので,出力層において,
という値が入って来ます.ここでニューロンはある閾値を越えないと発火しないため,
となり,この値がゼロ以上であれば発火ということで1を出力し, ゼロより小さければ発火しなかったということでゼロを出力します. よって入力と出力の関係は次のようになります.
ここでf(.)とはゼロ以上の値が入って来たときに1,それ以外ではゼロを返す関数です.
また,閾値を意識せずに処理することができるように,入力層においてN次元であれば, 仮想的にもう一つ常に1を出力するユニットを考えN+1次元にします,その仮想ユニットと出力層の ユニットとの荷重を閾値(-θ)と考えると,
となり,シンプルに記述できます.これは入力ベクトルと重みベクトルの内積を f(.)に渡しているとも考えられます.
それではANDを例に学習の手順を書いてみます.ANDとはプログラムにおける ANDやORのANDです.ANDの入出力は次のようになります.
入力が0(偽)と0(偽)ならば出力は0(偽) 入力が0(偽)と1(真)ならば出力は0(偽) 入力が1(真)と0(偽)ならば出力は0(偽) 入力が1(真)と1(真)ならば出力は1(真)
これは図で表すと次のように分離することになります.
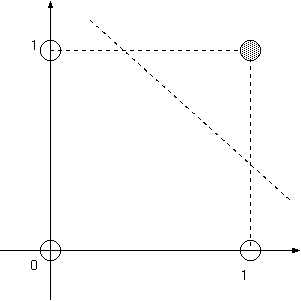
2次元で考えているので線で分離されていますが,一般的には超平面で分離される 事になります.
ここで,実際には閾値があるので多少座標は違っているのですが,
の式における重みwのベクトルが超平面の法線ベクトルとなり, (1,1)座標の領域の方を向いていることになります. ここで学習は次の式で行います.
ηは学習率といい1以下の正の定数です.tは教師データでoは入力に対するネットワークの 出力です.つまり,出力が正しければ(教師データと同じであれば)修正は行われず, 1を出力すべきところ(t=1)を0と出力すれば(o=0)結合荷重はηx減少させ, 0を出力すべきところ(t=0)を1と出力すれば(o=1)結合荷重はηx増加させます.
ここで,なんでベクトルの足し算と引き算で学習ができるのか疑問に思うかもしれません. 閾値の関係で多少違いますが, 例えば,間違って1が出力されたとき,次のようになっています.
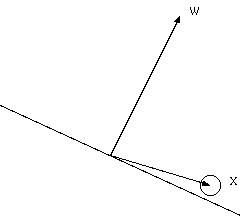
このときベクトルの引き算が行われるため,
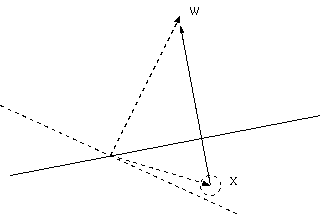
のように超平面が変化します.逆に間違って0が出力されたときも,
となっているのが,

のように変化します.
今回出力層のユニットが1つの単純パーセプトロンを考えましたが, 「出力が1のときクラスタ1に属する」,「出力が0のときクラスタ1に属さない」というふうに 考えると,単純パーセプトロンを組合せ,例えば数字の画像を識別しようとすれば,
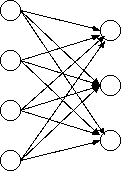
として,出力層の上から「数字が1のとき1,それ以外で0」,「数字が2のとき1,それ以外で0」・・・とすれば 一つ目の出力のみが1となったときに数字の1が書かれていたと認識することができそうです. ただし,超平面で領域を分割しなければいけないため,線型分離できない問題, 例えばXORのような問題はパーセプトロンでは解くことができません.
説明が長くなってしまいましたが,ソースコードは簡単です.
double StepFunction(double net)
{
return net < 0 ? 0 : 1;
}
これは説明中にf(.)として出てきた関数です.
void Forward(double *input, double *output,
int ni, int no, double wio[ni][no])
{
int i, j;
double net;
input[ni-1] = 1;
for(i=0; i<no; i++){
net = .0;
for(j=0; j<ni; j++){
net += wio[j][i]*input[j];
}
output[i] = StepFunction(net);
}
}
inputが入力層のベクトル,outputが出力層のベクトルです. ni,noはそれぞれ入力層,出力層のユニットの数で,wioは入力層と出力層の間の 結合荷重となります.input[ni-1]=1はinputの最後の要素を仮想ユニットとして 常に1を出力するようにしているからです.この関数によって入力に対する ネットワークの出力を得ることができます.
void Backward(double *input, double *output, int ni, int no,
double wio[ni][no], double eta, double *teacher)
{
int i, j;
for(i=0; i<no; i++){
for(j=0; j<ni; j++){
wio[j][i] += eta*(teacher[i] - output[i])*input[j];
}
}
}
Forwardの後に呼ぶことで学習が行えます. teacherとは教師データです.以上でパーセプトロンの関数は完成ですが, mainの方も多少解説しておきます.
double teacher[4][3] = {
{0, 0, 0},
{1, 0, 0},
{0, 1, 0},
{1, 1, 1}
};
これが教師データです.左から2つが入力,右の部分が対応する出力です. 今回ANDを学習させています.
for(i=0; i<INPUTSIZE; i++){
for(j=0; j<OUTPUTSIZE; j++){
weight_io[i][j] = ((double)rand()/RAND_MAX)/10;
}
}
INPUTSIZE,OUTPUTSIZEはそれぞれ入力層と出力層のユニット数, weight_ioは結合荷重で,0から0.1までの乱数で初期化しています. ここで入力層のユニットは仮想ユニットの分が含まれ3つになっていることに注意してください.
for(i=0; i<LOOPNUM; i++){
for(j=0; j<4; j++){
input[0] = teacher[j][0];
input[1] = teacher[j][1];
Forward(input, output, INPUTSIZE, OUTPUTSIZE, weight_io);
Backward(input, output, INPUTSIZE, OUTPUTSIZE,
weight_io, 0.01, &teacher[j][2]);
}
}
LOOPNUM回通り学習させています.線型分離可能な問題であれば, これが終わればネットワークがしっかりと構築されているはずですので, Forwardを使えば入力に対する理想的な出力が得られるハズです.