Karhunen-Loeve展開の略でベクトルの分布を最も良く近似する部分空間を求める方法です. 例えば5つの要素を持つベクトルがいくつかある場合に,出来るだけ元のデータを失わないように 3つや4つの要素のベクトルで表そうといった手法です.圧縮やパターン認識の分野で用いられたりしています. 要するに元のデータの特徴を残し,あまり特徴と関係ないであろう部分を消してしまおうという処理です.
具体的には,画像であれば100×100ピクセルのグレースケールの画像であれば, 10000個のデータを持っていますが,これは10000次元の1点で表すことができます. 実際には10000次元で表すとベクトルは1個になってしまいKL展開をすることができないので, 10×10のブロックに分けて100次元のベクトルが100個ある,などと考えて処理します. そして次元を例えば70次元などに落とす事で圧縮することができます.
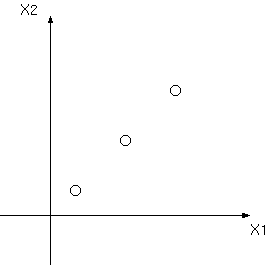
次元が高いとわかりづらいので2次元を1次元に落とすと考えてみます. 上のようにX1-X2軸で表される3つの点があるとします. そのとき例えば,
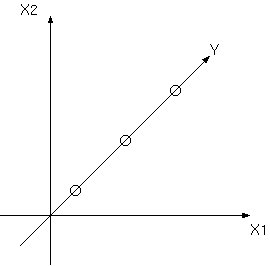
というY軸を考えるとまったくデータを損なわずに2次元から1次元に落とす事ができます. そのためこの3つの点はX1-X2座標系で表されているときには大きな無駄があったと言えます. しかし,次のように,
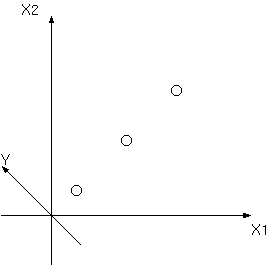
このようなY軸を考えると3つの点に違いが無くなってしまいます. そのため次元を下げる際にはどういう軸を選ぶかが大変重要となります.
実際に次元を削除するときに次元を下げてもデータが失われないという事は希で, ある基準を設け,その基準に沿ってできるだけ特徴を失わないようにしようとします. ここでは分散を考え,分散が最大になるように次元を削除していきます.分散とは 平たくいうと散らばり具合です.つまり,他との違いが大きい部分が特徴であり, 似たり寄ったりの部分は無くなってもいいだろうという観点です. 同じ色のものが沢山あるときに色で区別しようとしないのと同じ事です.
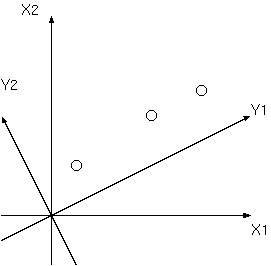
上のようにY1,Y2軸を考えたときに,Y1軸の方がY2軸よりも分散は大きくなります. Y1を選んだとしてもY1軸上に点が乗っているわけではないので, データは損なわれます.しかし,分散は最大になるので,元の特徴は残っていると 考えます.
元のデータの次元をd次元とし,次元削除後の次元をd'とします. d次元ベクトルxをd'次元ベクトルyに変換する為には,
とします.ここで行列Aは変換行列と呼ばれますが,行列Aを掛ける理由は 単純に5×3の行列と5次元のベクトルを掛けると3次元のベクトルになるからです. 行列が転置になっていますが,行列Aは変換後の座標系の正規直交基底となる ベクトルを並べたもので,ベクトルは通常縦に並べて表します. そのため掛けるときには転置にしないと計算ができません.とりあえず d=d'として分散を求めてみます.
ここで変換後のyベクトルの平均(平均ベクトル)m'は,変換前の xベクトルの平均ベクトルmを使い,
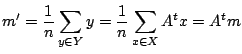
と表すことができます.これで分散が計算できるようになりました.
ベクトルの分散も普通の分散と同じような式で計算することができ, 次のような式になります.
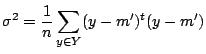
各ベクトルから平均を引き,2乗して総和を取ったものを個数で割っています. 通常の分散がベクトルに変わっただけです.ここで,
を用いて式変形すると,
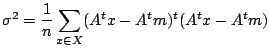
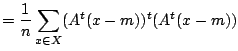
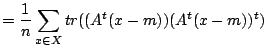
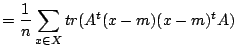
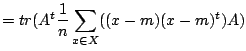
紛らわしいですが,ここでΣは数学記号でいう総和ではなく,
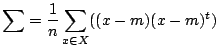
で表される共分散行列といわれるものです.
ここで行列Aが何でもいいのであれば要素を大きくすればいくらでも大きくなるわけですが, 行列Aは正規直交型のベクトルから成っています.そのため次の式を満たす必要があります. 行列Iは単位行列です.
この式を満たした上で分散を最大にするのですが,これは変分問題といい, この式の事を拘束条件といいます.ここで次式を考えます.
ここでΛはLagrange未定係数法におけるλに相当するものです.
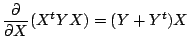
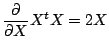
より,J(A)を行列Aで偏微分しゼロと置くと,
となり,変形して,
となり,このことから行列Aは共分散行列を対角化する行列であるとわかります. これを分散の式に代入すると,分散は変換後の次元の対角行列Λの対角成分の和であると言えます.
つまりここから言えることは,d次元をd'次元に落とす場合, 行列Aをd次元の正方行列だとして共分散行列を対角化し,固有値の大きい方から d'を残し,それに対応する固有ベクトルのみで作られる行列を変換行列とおけばいいという事です. 固有値や固有ベクトルはJacobi法で 求めることができます.また,Jacobi法の固有値のところで書いていますが, 固有値が大きい場合,対応する固有ベクトル成分が大きくなり,固有値が小さい場合は 対応する固有ベクトル成分が小さくなる,つまり,大きな特徴を残すという特性とも合致します.
KL展開の関数を作るにあたっていくつか関数を作成しています.
Matrix *MultMatrix(Matrix* matrix1, Matrix* matrix2); void TransposeMatrix(Matrix* matrix); static Matrix* AverageVector(Matrix *matrix); static void SortEigen(Vector *vec, Matrix *mat); static void ExchangeColumnvector(Matrix *m, int a, int b); static Matrix* CovarianceMatrix(Matrix *matrix);
MultMatrixは行列の掛け算をし,TransposeMatrixは転置行列をつくり, AverageVectorは引数の列ベクトルの平均ベクトルを返します. SortEigenは固有値が入ったvecを降順にソートし,それに対応するmatの 固有ベクトルを固有値に合わせてソートします.ExchangeColumnvectorは 行列mのa列とb列の列ベクトルを交換します.CovarianceMatrixは 列ベクトルの共分散行列を返します. これらの関数についてはソースコードを見てください.
上の関数を使ってKL展開をするKLEncodeと展開後のベクトルを 元の座標系に戻すKLDecodeを作成します.上での説明は長かったですが, 実装は意外と簡単です.
neweig = CreateMatrix(newdim, eigenvector->height);
cov = CovarianceMatrix(tempx);
eigennum = Jacobi(cov, eigenvector);
SortEigen(eigennum, eigenvector);
for(i=0; i<neweig->width; i++){
for(j=0; j<neweig->height; j++){
neweig->a[j*neweig->width+i] = eigenvector->a[j*eigenvector->width+i];
}
}
TransposeMatrix(neweig);
*x = MultMatrix(neweig, tempx);
TransposeMatrix(neweig);
for(i=0; i<eigennum->size; i++){
if(i >= newdim){
*error += eigennum->v[i];
}
}
先ずneweigにKL展開後の変換行列を入れる領域を確保します. その後共分散行列を作成,Jacobi法で対角化し,SortEigenで 固有値を降順にソートします.eigenvectorは次元を減らしていない状態の変換行列ですので, for文内で変換後の行列neweigの領域分だけeigenvectorからコピーすれば 変換後の次元分だけの固有ベクトルが残ります.
これを計算しあらたなベクトルを得るわけですが,元のベクトルは列ベクトルとして tempxの中にまとめられているため,行列のまま計算しています. 計算後は変換後のベクトルが列ベクトルとして格納されます. 最後のerrorはKL展開をすることによって失われた分散となります. そのため分散がゼロであれば,復元後に元に戻らなくても誤差はゼロになります. これは次元を削除することで失われた固有値の和となります. ここで上の式に左から変換行列Aを掛けると元のベクトルに戻すことができます.
void KLDecode(Matrix** x, Matrix* eig)
{
Matrix *temp;
temp = MultMatrix(eig, *x);
FreeMatrix(*x);
*x = temp;
}
ソースコードはこのようになります.