Jacobi法(ヤコビ法)を用いて行列の固有値と固有ベクトルを求めてみたいと思います. Jacobi法では対称行列しか扱えないという制約があるものの,アルゴリズム自体も簡単な上に,解が必ず実数になる事もあり,大変シンプルです.
任意のn次正方行列Aに対し,
が成り立つときλを固有値,xを固有ベクトルという.
つまり,あるベクトルxに行列Aを掛けるとベクトルxが定数倍になるという意味で,ベクトルの向いている方向は変化しないという事です.また,n次の正方行列には固有値は重解を含めるとn個存在し,それに対応する固有ベクトルもn個存在します.固有ベクトルを基底とするとき,行列Aを乗ずると,各固有ベクトルの成分は対応する固有値倍されますので,固有値の絶対値が大きい固有ベクトル成分は大きく,小さい固有ベクトル成分は小さくなり,何度も乗ずると0に向かって行きます.
となるとき,行列Aと行列Bの固有値は一致します.また,行列Aが対称行列である場合,直交行列Pを用いて
と,対角化することができ,行列Λの対角成分は行列Λの固有値となります.ここで直交行列Pの列ベクトルとそれに対応する行列Λの列の対角成分は固有値と固有ベクトルの関係となります.
このことから行列Aの固有値と固有ベクトルを求めるには,行列Aを対角化する直交行列Pを求めれば良いことになります.
Jacobi法ではこの直交行列Pを反復作業で求めています.つまり,行列Aの非対角成分の1つをゼロにする直交行列を用い,
とする事を繰り返します.
これを繰り返し全ての非対角成分をゼロにし,対角化をするのがJacobi法です.また,
この部分が行列Aを対角化する直交行列であり,列ベクトルは固有ベクトルとなります.
まず,行列Aの非対角成分の中から絶対値が最大の成分を探します.その成分がp行q列(p < q)だったとすると,直交行列Pは

のように,単位行列のpp成分をcosに,pq成分をsinに, qp成分を-sinに,qq成分をcosに置き換えたものを考え,
を考えたときに行列Aのpq,qp成分がゼロになるようにします.
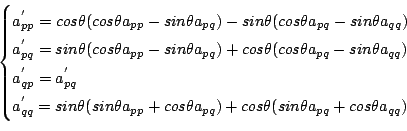
この4成分は展開すると上のようになり,pq,qp成分をゼロにするので,
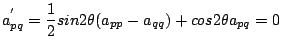
となり,
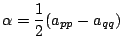
とおくと,
また,
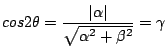
とすると,
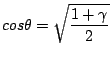
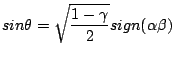
となります. sign(αβ)とはαとβの積が正であればsinも正になり,積が負であれば sinも負になるという意味です.これは実際計算してみればわかりますが,計算の途中でcos2θのルートを取る部分があります.このときcosを正に固定したため,
により,sinの符号がαβによって変化しています.
その他値が変わるのは次の式で表されるものだけで,それ以外は変化しません.
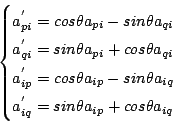
それではソースコードを見ていきます.ほとんど上の式を放りこんだだけです.
for(i=0; i<eigenvectors->width; i++){
for(j=0; j<eigenvectors->height; j++){
if(i==j) eigenvectors->a[i*eigenvectors->width + j] = 1;
else eigenvectors->a[i*eigenvectors->width + j] = 0;
}
}
eigenvectorsを単位行列になるように初期化しています.これに対して右側から次々と直交行列を乗ずる事で最終的にこれが行列Aを対角化する直交行列となり,各列には固有ベクトルが入ります.
if(!(max = GetMaxvalue(matrix, &p, &q))) break; app = matrix->a[p*matrix->width + p]; apq = matrix->a[p*matrix->width + q]; aqq = matrix->a[q*matrix->width + q];
ここからループに入ります. GetMaxvalueによって絶対値が最大の非対角行列成分の値maxと列番号p,行番号qを得ます.このmaxの値がdefineで指定している許容誤差以内になったらループを抜けることになります.
alpha = (app - aqq)/2; beta = -apq; gamma = fabs(alpha)/sqrt(alpha*alpha + beta*beta); s = sqrt((1 - gamma)/2); c = sqrt((1 + gamma)/2); if(alpha*beta < 0) s = -s;
上の式の通り値を設定しています.
for(i=0; i<matrix->height; i++){
temp = c*matrix->a[p*matrix->width + i] - s*matrix->a[q*matrix->width + i];
matrix->a[q*matrix->width + i] =
s*matrix->a[p*matrix->width + i] + c*matrix->a[q*matrix->width + i];
matrix->a[p*matrix->width + i] = temp;
}
for(i=0; i<matrix->height; i++){
matrix->a[i*matrix->width + p] = matrix->a[p*matrix->width + i];
matrix->a[i*matrix->width + q] = matrix->a[q*matrix->width + i];
}
matrix->a[p*matrix->width + p] = c*c*app + s*s*aqq - 2*s*c*apq;
matrix->a[p*matrix->width + q] = s*c*(app-aqq) + (c*c - s*s)*apq;
matrix->a[q*matrix->width + p] = s*c*(app-aqq) + (c*c - s*s)*apq;
matrix->a[q*matrix->width + q] = s*s*app + c*c*aqq + 2*s*c*apq;
式の通りなのですが,1つ目のfor文の1行目でわざわざtempに代入してから3行目で代入し直しているのは 1行目でそのまま代入してしまうと2行目の値が変わってしまうからです.
for(i=0; i<matrix->height; i++){
temp = c*eigenvectors->a[i*eigenvectors->width + p] -
s*eigenvectors->a[i*eigenvectors->width + q];
eigenvectors->a[i*eigenvectors->width + q] =
s*eigenvectors->a[i*eigenvectors->width + p] +
c*eigenvectors->a[i*eigenvectors->width + q];
eigenvectors->a[i*eigenvectors->width + p] = temp;
}
直交行列Pの更新です.行列Aよりも処理が少ないのは,Pは右側からしか乗じないからです.