フーリエ変換を使えば関数を時間軸から周波数軸に変換することができます.こんなことをして何が嬉しいかというと,時間によっていろんな物が変化しますが,周波数軸の方が扱いやすい場合が多く存在するためです.画像や音声など用途は様々です.また,フーリエ変換は可逆変化であるため,周波数軸で処理をし,時間軸に戻すという事ができるため大変重宝します.
具体的にフーリエ変換が何をしているかというと,全ての関数を正弦波の組合せだけで表そうとしています.角周波数と時間を掛ければ角度がでますので,いろいろな角周波数の正弦波を足したり引いたりしてそれぞれの角周波数の正弦波の重みを考えます.こんなとんでもない事を考えた人は凄いとしか言いようがないですが,使うだけならばそんなに難しくありません.公式に当てはめるだけです.
まず,フーリエ変換を適用するためには周期関数でなければなりません.つまりある一定の時間で繰り返される関数です.しかしフーリエ変換では関数の周期を無限大にすることで全ての関数が周期関数であるとみなします.フーリエ変換とその逆演算である逆フーリエ変換の式は次のようになります.
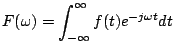
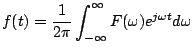
しかしこれをプログラムで実装しようとすると問題があります. PCでは無限大を扱うことはできませんし,連続の値をとることができません.そのためプログラムで実装するときにはフーリエ変換に離散の概念を適用した離散フーリエ変換を使います.離散フーリエ変換と逆離散フーリエ変換は次のようになります.
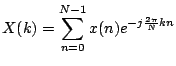
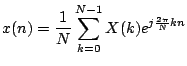
ここでオイラーの公式を使います.
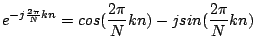
こうすることで後は四則計算だけになります.
if(flag==-1)coefficient=num;
else coefficient=1;
for(i=0; i<num; i++){
for(j=0; j<num; j++){
temp_re[i] +=
re[j]*cos(2*PI*i*j/num) + flag*im[j]*sin(2*PI*i*j/num);
temp_im[i] +=
-flag*re[j]*sin(2*PI*i*j/num) + im[j]*cos(2*PI*i*j/num);
}
temp_re[i] /= coefficient;
temp_im[i] /= coefficient;
}
離散フーリエ変換の式においてx(k)は実数,X(k)は複素数ですが, x(k)の方を虚数の値がゼロとして計算しています.これは離散フーリエ変換も逆フーリエ変換も式の違いが符号と係数だけであるため,フラグを使って分岐させる事で1つの関数で2役演じています.ただし,この離散フーリエ変換,逆フーリエ変換の式は,本来周期の区間が, -N/2からN/2であったのを0からN-1にシフトしているため,実際にこの関数を使う前後でデータの中央より右側と左側を入れ換える必要があります. (データの両端が中央になります.)計算して得られるデータは端程周波数が低く,中央になる程周波数が高くなります.