せっかくLU分解を作ったのでそれを用いて連立一次方程式を解いてみます. LU分解を使って連立一次方程式が解けるということはLU分解 のところで書きましたので併せて見てください.例えば係数の行列が3×3であれば,
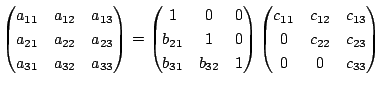
のように下三角行列Lと上三角行列Uに分解でき,
という連立一次方程式であれば,
を解くことと等価となります.ここでベクトルcを考え,
とおくと,
となりますが,このベクトルcを求める事を前進代入といいます.cが求まると次に
より,ベクトルxを求めることが出来ます.これを後退代入といいます.
行列matrixとベクトルansは引数として受け取った係数行列とyベクトルです.
order = LU(matrix);
for(i=0; i<ans->size; i++){
if(i != order[i]){
tempd = ans->v[order[i]];
ans->v[order[i]] = ans->v[i];
ans->v[i] = tempd;
order[order[i]] = order[i];
order[i] = i;
}
}
LU分解の計算中に都合がいいように行を入れ換えられるので, どの行とどの行が入れ換えられたかわかるように,例えば0行目と2行目が入れ換えられれば, orderは2,1,0,3,4・・・となっています.そのため,それに合わせるために ベクトルansの方も入れ換えます.
for(i=1; i<height; i++){
for(j=0; j<i; j++){
ans->v[i] -= ans->v[j]*matrix->a[i*width + j];
}
}
それでは前進代入です.下三角行列である行列Lは対角成分が1なので, 他の項を引いてやるだけです.これでベクトルansはベクトルcになりました.
for(i=height-1; i>=0; i--){
if(!(matrix->a[i*width + i])){
fprintf(stderr, "Error In FBSubstitution.\n");
exit(1);
}
ans->v[i] /= matrix->a[i*width + i];
for(j=i-1; j>=0; j--){
ans->v[j] -= ans->v[i]*matrix->a[j*width + i];
}
}
ここで後退代入を行っています.後退代入は前進代入と違って対角成分がまちまちなので, 他の項を引いた後に対角成分で割る必要があります.そのためゼロでないかのチェックが必要になります.