積分ができるようになったので微分もできるようにしてみたいと思います. 微分の方法にもいろいろあるようですが,ここでは一番簡単に, 微分の基本式を使って求めてみたいと思います. かなり単純明快で簡単に実装できますが,その分誤差が大きいです.
導関数の定義とは,
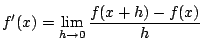
で表されます.一見王道の様ですが,PCにおいて無限を扱うことができませんので, 当然hは「PCでの小数で表現できる範囲内での出来るだけ小さな値」ということになります. なのでこの値の設定の仕方で誤差は多少小さくできるものの,小数点3桁あたりに 誤差が出てきたりと無視し難い誤差が発生する場合があります. 厳密に求めたい場合はこの方法は使えませんが,ドンブリ勘定でいいなら 結構便利な方法です.
double Derivative(double (*f)(double t), double x, double dx)
{
return ((*f)(x + dx) - (*f)(x))/dx;
}
たったの1行で実装できました. あまりに単純ですが,どの程度誤差がでるのかいくつか見てみます.
$ ./calculation_samp x*x :f'(2) 4.000000 exp(x):f'(1) 2.718314 cos(x):f'(PI/2) -1.000000 log(x):f'(2) 0.500000
これを見てみると結構よさそうな結果になっています. ただし,expに関しては,exp(1)が2.718281・・・ である事を考えると,あまり小さな誤差ではなさそうです. とは言え,複雑な式の微分係数を求める場合でも有効ですので, あまり精度が要求されない場合は便利だと思います.