物にはいろいろな特徴がありますが,それをコンピュータによって識別させてみたいと思います. 識別させるものは,顔だったり,コインだったりと様々ですが, 例えば,物の大きさ,長さ,色,重さなどを数値としてそれぞれをベクトルの要素とします. こうしてできあがったベクトルは特徴ベクトルと呼ばれます.またパターンとも呼ばれます.
他にも顔や文字等を識別しようとすれば,それらを画像として取り込み, そのピクセルを任意に並べてピクセル値のベクトルを作れば特徴ベクトルにすることが できます.
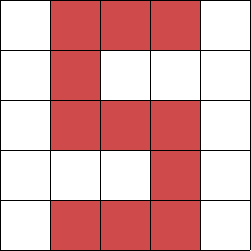
例えば「5」という数字であれば,上のようになっているでしょうが, 文字はフォントによって形も多少変わってきますし,自筆などであれば, 書き手によっても形が違うでしょう. そのため,判別させたい数字ごとに数サンプルずつ用意し,未知の特徴ベクトルが 与えられたときに,各サンプルに基づいて未知のものがどの数字に属するのかを判断させます. このとき,各数字におけるサンプルの集まりのことをクラスタといいます.
コンピュータにこのような判断をさせる方法は数多くありますが, 一番簡単で直感的な方法では最近傍決定則があります.これは英語でNearest Neighbor Ruleと いうことから略してNN法とも呼ばれます.
最近傍決定則では未知パターンがどのクラスタに属するかを判断させる方法として, 座標において未知パターンと一番距離の近いサンプルを探します. そうして見つけたサンプルが属するクラスタに未知パターンも属するハズであると考えるものです.
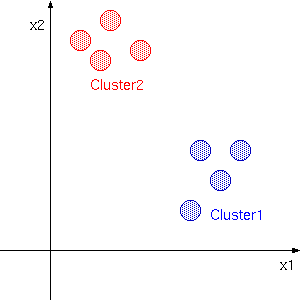
上の図は便宜上2次元となっていますが,特徴ベクトルは普通高次のベクトルとなります. しかし,次元が増えるだけで考えは同じです.
わかりやすいので文字の識別で考えてみます. 上の図でCluster1を「あ」という文字のサンプル. Cluster2を「い」という文字のサンプルだとします. これらのデータはあらかじめコンピュータに与えておく必要がありますが, ここで,
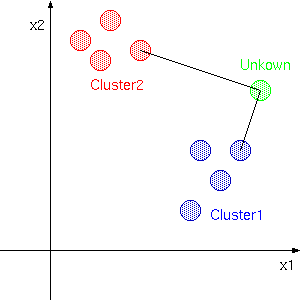
のように未知パターンが与えられたとします. それぞれのクラスタのサンプルで未知パターンと一番近いものを 黒の実線で描いていますが,未知パターンに近いのは Cluster1の方です.そのため未知パターンはCluster1に属するであろうと 考え,未知パターンの表す文字は「あ」であると判断します.
これが最近傍決定則ですが,ここで未知パターンが全てのサンプルと極端に離れている場合を 考えてみます.例えば,Cluster1とCluster2だとCluster1の方が近いことは近いが, 余りに離れ過ぎている場合です.未知パターンが絶対に2つのうちどちらかに属するのであれば, Cluster1だと判断してもいいかもしれませんが,そうでなければ,どちらかに属するのではなく, 新たな別のものかもしれません.そのため,そのクラスタに属すると判断できる 最大の距離を決め,それを越えていたら「よくわからないパターンが来た」ということで, さじを投げさせる事にします.
それではソースコードを見てみます. パターンを扱うために,ベクトルを使いますが,いくつかのベクトルの集合を クラスタとして保持しなければならないので,新たにClusterという構造体を定義します.
typedef struct{
int num;
int dimension;
Vector **v;
}Cluster;
このようにベクトルへのポインタへのポインタを保持していると ベクトルのポインタを複数一括に扱えて便利です. 同時にクラスタ内のベクトルの数をnumで,ベクトルの次元をdimensionで保持しておきます.
Cluster *CreateCluster(int num, int dimension)
{
Cluster *temp;
int i;
if((temp = (Cluster*)malloc(sizeof(Cluster))) == NULL){
fprintf(stderr, "Cannot Create New Cluster\n");
exit(1);
}
if((temp->v = (Vector**)malloc(sizeof(Vector*)*num)) == NULL){
fprintf(stderr, "Cannot Create New Cluster\n");
exit(1);
}
for(i=0; i<num; i++){
temp->v[i] = CreateVector(dimension);
}
temp->num = num;
temp->dimension = dimension;
return temp;
}
それではクラスタを作成するCreateClusterを作成します.クラスタに属するベクトルの個数numと ベクトルの次元dimensionを引数にとります. まず,クラスタのための領域を確保し,ベクトルのポインタをまとめて保持するための領域を確保します. そのあとでそれぞれのベクトルの領域を確保します.
void FreeCluster(Cluster *c)
{
int i;
for(i=0; i<c->num; i++){
FreeVector(c->v[i]);
}
free(c->v);
free(c);
}
領域を開放するときはFreeClusterを使います.確保したときの逆順に開放していきます.
それでは最近傍決定則を作ります.
int NNrule(Cluster **cluster, int num, Vector *x, double maxd)
{
int i, j, k;
int minindex=0;
double d, min=0.0;
for(k=0; k<cluster[0]->v[0]->size; k++){
min += SQR(x->v[k] - cluster[0]->v[0]->v[k]);
}
for(i=0; i<num; i++){
for(j=0; j<cluster[i]->num; j++){
d = 0.0;
for(k=0; k<cluster[i]->v[j]->size; k++){
d += SQR(x->v[k] - cluster[i]->v[j]->v[k]);
}
if(min > d){
min = d;
minindex = i;
}
}
}
if(min > SQR(maxd)) return -1;
return minindex;
}
引数はクラスタへのポインタへのポインタ,クラスタの数,未知パターン,最後に 最短の距離がどこまでならそのクラスタに属するかを指定するmaxdをとります. クラスタへのポインタへのポインタを引数に取る理由は,最近傍決定則を使う場合に, クラスタを複数渡す必要があるからです.そのため配列などで一括に扱い, NNruleにはそのアドレスを渡したいところです. しかし,Clusterはそもそもポインタで処理をしているため, ポインタの配列で扱う事になります.そのため,配列のアドレスを渡すと Clusterのポインタのポインタとなります.
最初のfor文で最短距離がゼロ番目のクラスタの1つ目のベクトルで初期化し, そのあと3重forループで一番近いベクトルの属するクラスタを探します. 最後にその最短距離がmaxdより大きければ,属するクラスタは無かったということで,