画像をフーリエ変換する場合であれば,そこまで大きくない画像であれば通常の離散フーリエ変換でも我慢できる程度の時間で処理をすることができますが, PCの性能が優れているとはいえ,音声のようにデータが膨大になってくるとそうもいきません.そこでデータの数が2の累乗でなければならないという制約ができますが,高速に処理することができる高速フーリエ変換を導入したいと思います.
まず通常の離散フーリエ変換の式を見てみます.
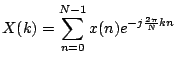
ここで
とし,一つ目の式を行列で表してみます.一般的に書けるのですが,簡単のためデータを8個として書いてみます.

このとき
を使うと次のようになります.
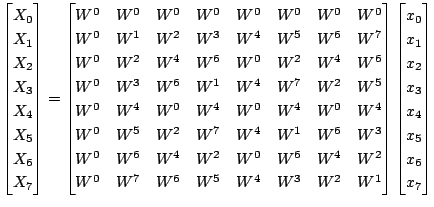
ここで上の行列の真ん中で左右に分けて考えると,添字が偶数の行については左と右の部分が同じで,添字が奇数の行については左と右の部分が半周期ずれたものになっているのがわかります.そのため上の式は以下と等価です.
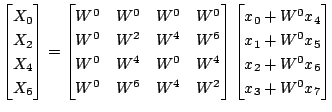
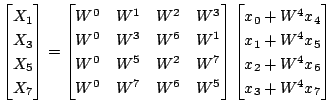
同じようすると最終的に次のようになります.
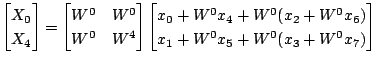
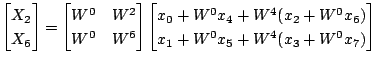
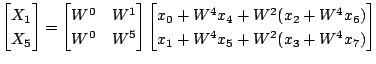
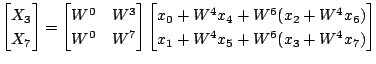
これを図で表すと次のようになります.
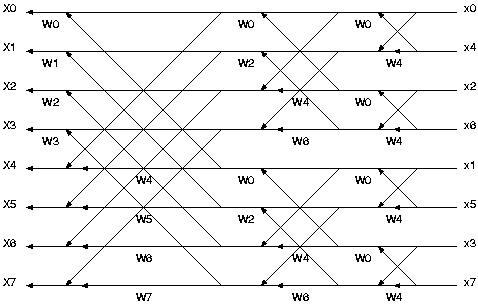
図1
図1を見てもわかる通りxの並びが変わっています.このように並び替えることで計算がしやすくなります.それではソースコードを見てみます.
dfttimes = num;
power = power_two(num); //2の何乗かを返す
for(i=0; i<power-1; i++){
indexto = offset = 0;
while(indexto < num){
indexfrom = 0;
while(indexfrom < dfttimes){
rbuf[indexto] = re[indexfrom + offset];
ibuf[indexto] = im[indexfrom + offset];
indexto++;
indexfrom += 2;
if(indexfrom == dfttimes) indexfrom = 1;
}
offset += dfttimes;
}
for(j=0; j<num; j++){
re[j] = rbuf[j];
im[j] = ibuf[j];
}
dfttimes /= 2;
}
re, im, numは引数として渡されています.それぞれフーリエ変換するためのデータの実数部と虚数部,データの個数です.この部分では渡された配列のデータを上の図1のxのように並び替えています.
ここから少しソースがごちゃごちゃとするのですが,上の図1の右から左へループをしながら計算しているに過ぎません.
unit_angle = 2.0 * PI / newnum;
dft = 2;
for(i=0; i<power; i++){
dftnum = newnum / dft;
step_angle = unit_angle * dftnum;
for(j=0; j<dftnum; j++){
angle = 0.0;
for(k=0; k<dft; k++){
indexto = j*dft + k;
if(k < dft/2){
indexfrom1 = indexto;
indexfrom2 = indexfrom1 + dft/2;
}else{
indexfrom2 = indexto;
indexfrom1 = indexto - dft/2;
}
rbuf = re[indexfrom2];
ibuf = im[indexfrom2];
temp_re[indexto] =
re[indexfrom1] + rbuf*cos(angle) + flag*ibuf*sin(angle);
temp_im[indexto] =
im[indexfrom1] + ibuf*cos(angle) - flag*rbuf*sin(angle);
angle += step_angle;
}
}
for(j=0; j<newnum; j++){
re[j] = temp_re[j];
im[j] = temp_im[j];
}
dft *= 2;
}
図1で矢印が交差している部分が視覚的に右から左へ3つのグループに分けられそうです.また右から左へ順に上下に4つ,2つ,1つというふうに分けられそうです.変数のdftはこの1つのグループに属するxの数となり,dftnumがそのグループの数と言えます.なので最初はそれぞれ2と4となります.
行列においてみられる対称性を利用し演算回数を減らしてきましたが,データの数が2の累乗でなければこれができなくなってしまいます.